[백준/코틀린] 1967번: 트리의 지름

링크

1967번: 트리의 지름

풀이

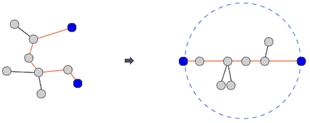
트리의 지름은 트리에서 존재하는 모든 경로 중 가장 긴 경로의 길이입니다.

트리의 지름

트리는 사이클이 없고 모든 정점이 연결되어 있으므로,
두 정점 사이의 경로는 항상 하나로 결정됩니다.
따라서 DFS 또는 BFS로 누적 거리를 계산하면, 각 정점까지의 거리를 구할 수 있습니다.

임의의 정점에서 가장 먼 정점을 A라고 하면,
A는 반드시 지름의 한 끝점이 됩니다.
그리고 A에서 가장 먼 정점 B를 구하게 되면,
두 정점 A와 B는 트리 지름의 양 끝점이 됩니다.

즉, 두 번의 탐색을 통해 트리의 지름을 구할 수 있습니다.

코드

var n = 0
lateinit var graph: List<MutableList<Pair<Int, Int>>>
lateinit var distance: IntArray
lateinit var visited: BooleanArray

fun dfs(start: Int): Int {
    val stack = ArrayDeque<Pair<Int, Int>>()
    distance = IntArray(n + 1)
    visited = BooleanArray(n + 1)
    var (max, index) = 0 to 0

    visited[start] = true
    stack.addLast(start to 0)
    while (stack.isNotEmpty()) {
        val (cur, cd) = stack.removeLast()

        distance[cur] = cd
        if (max < cd) {
            max = cd
            index = cur
        }
        graph[cur].forEach {
            val next = it.first
            val nd = it.second + cd

            if (!visited[next]) {
                visited[next] = true
                stack.addLast(next to nd)
            }
        }
    }

    return index
}

fun main() {
    n = readln().toInt()
    graph = List(n + 1) { mutableListOf() }

    repeat(n - 1) {
        val (u, v, w) = readln().split(" ").map { it.toInt() }

        graph[u] += v to w
        graph[v] += u to w
    }

    val a = dfs(1)
    val b = dfs(a)

    println(distance[b])
}