[백준/코틀린] 11659번: 구간 합 구하기 4

링크

11659번: 구간 합 구하기 4

풀이

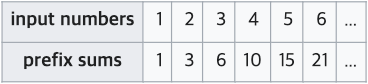
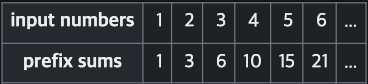
배열의 모든 인덱스까지의 누적 합을 미리 계산해
누적 합(prefix sum) 배열을 만들어두면,
구간 [i, j]의 합을 O(1)에 구할 수 있습니다.

출처: Wikipedia: Prefix sum

예를 들어, 위와 같이 누적 합 배열을 미리 계산해 두었다면,
구간 [3, 5]의 합은 다음처럼 구할 수 있습니다.

• prefixSum[5]: 5번째 원소까지의 누적 합 (1 + 2 + 3 + 4 + 5)
• prefixSum[2]: 2번째 원소까지의 누적 합 (1 + 2)

$\text{sum}[3, 5] = \text{prefixSum}[5] - \text{prefixSum}[2] = 12$

코드

fun main() {
    val (n, m) = readln().split(" ").map { it.toInt() }
    val nums = readln().split(" ").map { it.toInt() }
    val prefixSum = nums.scan(0) { acc, num -> acc + num }

    repeat(m) {
        val (i, j) = readln().split(" ").map { it.toInt() }

        println(prefixSum[j] - prefixSum[i - 1])
    }
}

연관 문제

• [백준/코틀린] 11660번: 구간 합 구하기 5 - 2차원 누적합